本文主要讲解 LeetCode 中第 75 号问题 Sort Colors 的解法,提供三种思路。
1. 题目描述
给定 n 个标记颜色的元素数组 nums(颜色有:红、白、蓝),对它们进行排序,使得相同颜色的元素相邻,颜色顺序:红、白、蓝,并且分别用 0、1、2 表示红、白、蓝。
条件限制:
- n == nums.length
- 1 <= n <= 300
- nums[i] 只可能是 0、1、2 三个中的一个
示例:
1
2
Input: nums = [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]
2. 求解思路
本题可以使用排序和基于三路快排的两类思路,并重点介绍基于三路快排的这种方式,所有代码均已经上传至 GitHub 中。
2.1 使用排序接口
因为颜色的顺序要求是:红、白、蓝,而红、白、蓝对应的数值大小是:0、1、2 ,所以对颜色进行排序,即相当于对数值进行排序。故最简单的方法是,直接使用编程语言提供的排序接口。如果颜色的顺序与其对应的数值大小关系不一致时,则需要自定义 Compare 接口。
1
2
3
4
5
class Solution1 {
public void sortColors(int[] nums) {
Arrays.sort(nums);
}
}
2.2 使用计数排序
因为颜色的种类有限,只有三种 ,因此可以使用计数排序。具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution2 {
public void sortColors(int[] nums) {
int[] colorCount = new int[3]; // 各个颜色出现的次数
// 统计各个颜色出现的次数
for (int i : nums) {
++colorCount[i];
}
// 按照颜色的顺序,重新排放元素
for (int i = 0; i < colorCount[0]; ++i) {
nums[i] = 0;
}
for (int i = 0; i < colorCount[1]; ++i) {
nums[colorCount[0] + i] = 1;
}
for (int i = 0; i < colorCount[2]; ++i) {
nums[colorCount[0] + colorCount[1] + i] = 2;
}
}
}
2.3 使用三路快排思路
在三路快排中,使用两个指针,将数组分成三个区间(大于元素 e ,等于元素 e ,小于元素 e)。而在此题中,三个颜色刚好对应三个区间,因此可以采用三路快排的思路,即使用两个指针,将数组划分成红、白、蓝(0、1、2)三个颜色区间。
使用指针 zero 标记 0 区间的结束位置,two 指针标记 2 区间的开始位置,指针 i 遍历数组。
指针 i 指向的元素存在如下三种情况:
- 等于 1 :则该元素不进行移动,指针 i 向后移动一步,如下图的情况 1 所示
- 等于 2:则该元素与 nums[two - 1] 交换,即将该元素移到 2 区间,然后指针 two 向前移到一步,指针 i 不移动(因为元素 nums[two - 1] 未处理),如下图的情况 2 所示
- 等于 0:则该元素与 nums[zero + 1] 交换,即将该元素移到 0 区间,然后指针 zero 向后移动一步,同时指针 i 也要向后移动一步,如下图的情况 3 所示
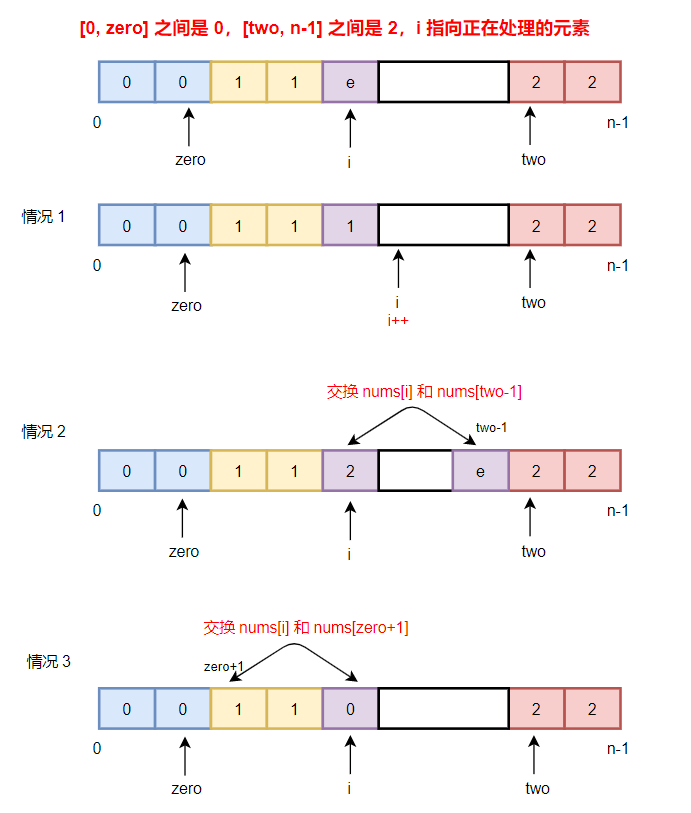
图中,蓝色区间表示 0 区间,全部都是 0;黄色区间表示 1 区间,全部都是 1;红色区间表示 2 区间,全部都是 2;紫色表示正处理的元素或未知的元素。
具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution3 {
public void sortColors(int[] nums) {
int zero = -1; // [0, zero] 之间是 0
int two = nums.length; // [two, n-1] 之间是 2
for (int i = 0; i < two; /* empty */) {
if (1 == nums[i]) {
++i;
} else if (2 == nums[i]) {
// 交换 nums[i]、nums[two-1]
int tmp = nums[i];
nums[i] = nums[two - 1];
nums[two - 1] = tmp;
--two;
} else if (0 == nums[i]) {
// 交换 nums[i]、nums[zero+1]
int tmp = nums[i];
nums[i] = nums[zero + 1];
nums[zero + 1] = tmp;
++i;
++zero;
}
}
}
}
3. 总结
在处理排序问题时,当待排序的元素种类较少时,可以使用计数排序。而对于此问题而言,由于元素只有三种,较简单,因此可以使用三路快排的思路解决。